Да-да, действительно существует теорема с таким названием. В чем заключается суть теоремы и почему она так называется и будет рассмотрено в этой статье.
Теорема ЧикенМакнаггетса была создана Анри Пиччиотто в 1980-х годах, когда он обедал в ресторане Макдоналдс вместе со своим сыном. Тогда наггетсы продавались упаковками по 6 и 9 штук, и Анри решил узнать, какое максимальное количество наггетсов невозможно купить. Он решил эту задачу на салфетке и получил, что при взаимно простых  и
и  , решение задачи заключаться в решении
, решение задачи заключаться в решении  . В дальнейшем он включил эту теорему в свой учебник по алгебре.
. В дальнейшем он включил эту теорему в свой учебник по алгебре.
Формальное определение теоремы: для любых двух взаимно простых положительных целых чисел 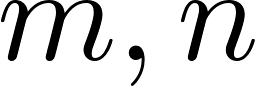 наибольшее целое число, которое не может быть записано в форме
наибольшее целое число, которое не может быть записано в форме  для неотрицательных целых чисел
для неотрицательных целых чисел  , равно
, равно 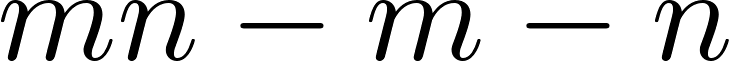 .
.
Сначала кажется, что эта теорема бесполезна в реальной жизни, однако теоремы такого типа часто применяются в задачах, связанных с расчетом денег. Например, какую максимальную сумму невозможно собрать используя только монеты с номиналом 3 и 7 единиц (ответ: 11). И на самом деле, теорема Чикен МакНагеттса всего-лишь частный случай проблемы монеты Фробениуса.
На этом познавательная часть теоремы закончилась и можно перейти к более серьезным вещам.
Доказательство теоремы
Определение: Количество  можно купить, если
можно купить, если  .
.
Требуется доказать, что  - это наибольшее количество, которое невозможно купить. Для этого необходимо доказать, что:
- это наибольшее количество, которое невозможно купить. Для этого необходимо доказать, что:
-
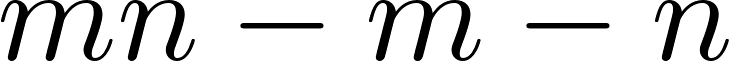 количество, которое невозможно купить.
количество, которое невозможно купить.
-
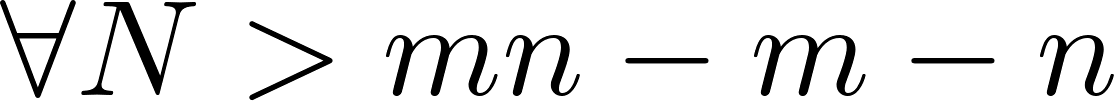 можно купить.
можно купить.
Доказательство:
Лемма 1: Пусть  множество решений уравнения
множество решений уравнения 
Доказательство леммы 1:
По теореме Безу:  . Легко проверить, что
. Легко проверить, что 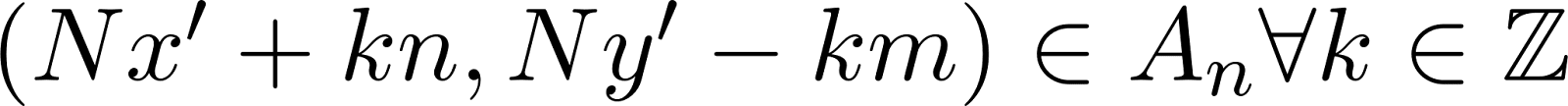 . Докажем, что других значений множества
. Докажем, что других значений множества  нет. Предположим, что
нет. Предположим, что 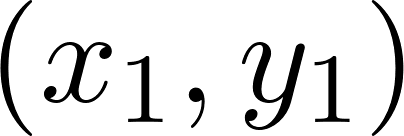 и
и 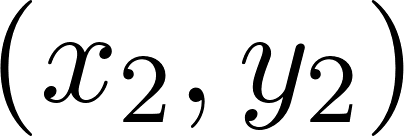 решение
решение  . Тогда
. Тогда  . Поскольку
. Поскольку  и
и 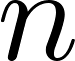 взаимно просты
взаимно просты 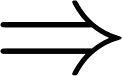
 делится на
делится на  ,
,  делится на
делится на 

 . Аналогично
. Аналогично  . Положим
. Положим  . Тогда
. Тогда 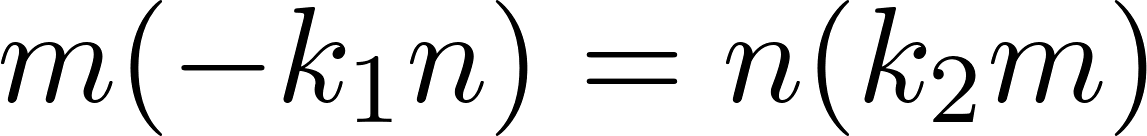


Лемма 2: 

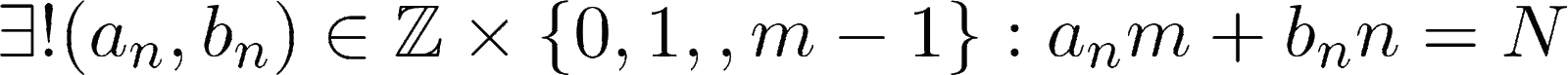
Доказательство леммы 2:
По алгоритму деления  .
.
Лемма 3: 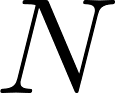 можно купить
можно купить 
Доказательство леммы 3:
Если  , тогда можно выбрать
, тогда можно выбрать 
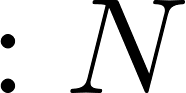 будет можно купить. Если
будет можно купить. Если 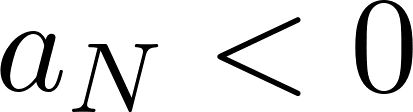 , тогда
, тогда 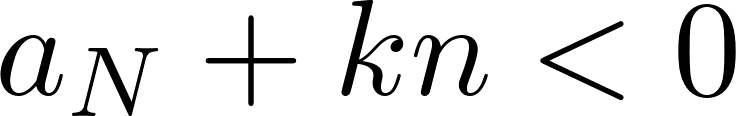 при
при  и
и  при
при  ,
,  одна из
одна из 

Таким образом набор непокупаемых чисел находится в  . Найдем максимум из этого набора. Так как
. Найдем максимум из этого набора. Так как  , максимум достигается, когда
, максимум достигается, когда 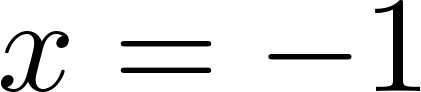 и
и 

 .
.
(Доказательство было взято и переведено отсюда)

