Посвящено моим друзьям, которые будут читать эту статью :)

История
Вообще, комплексные числа появились еще в в XVI веке, когда математики пытались решить кубические уравнения с отрицательными дискриминантами.
Изначально было мнение, что комплексные числа появились при решении пытливыми умами математиков квадратных уравнений. Но на самом деле, это далеко от правды. В реальности при решении квадратного уравнения х^2 = kx + b геометрически на координатной плоскости представляется, как пересечение параболы и прямой, при этом возникает 3 варианта:
- парабола не пересекает прямую
- парабола касается прямой
- парабола пересекает прямую в 2-х местах
Поэтому с точки зрения математики здесь все было честно и у математиков не было мотивации искать мнимые корни из отрицательных чисел.

Все поменялось при решении кубических уравнений, в которых прямая всегда пересекает кубическую параболу. Но при этом в при аналитическом решении уравнения возникают ситуации, когда приходится извлекать корни из отрицательного числа, даже если уравнение имеет вещественные корни.

Понятие комплексного числа
Прежде чем перейти к определению комплексного числа необходимо сделать дисклеймер: не пытайтесь представить комплексное число в жизни - это тоже самое, что попытаться представить 4-ое измерение пространство в нашем бренном трехмерном мире. Комплексные числа необходимы в математике, для того, чтобы определить ту область чисел, которую нельзя отобразить через вещественные числа.

Пока звучит непонятно, так что давайте разбираться.
Комплексное число имеет вид  и стоит заметить, что это единое число, а не сложение. Но при этом все комплексные числа имеют геометрическую интерпретацию и представляется на комплексной плоскости:
и стоит заметить, что это единое число, а не сложение. Но при этом все комплексные числа имеют геометрическую интерпретацию и представляется на комплексной плоскости:

Комплексная плоскость состоит из двух осей:
– Re - действительная ось
– Im - мнимая ось
Здесь все также как в геометрии 6-8 класса. Для примера построим 3 точки:




Корни n-й степени из единицы
Самый частая ситуация при которой используются комплексные числа - это простое извлечение корней из отрицательных чисел, поэтому рассмотрм примеры того, как это делается.
Начнем с простого примера:
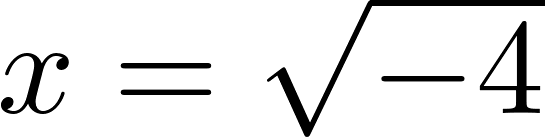
Нельзя извлечь корень? В действительных числах здесь действительно не будет решений. В комплексных числах извлечь корень можно. А точнее даже два!
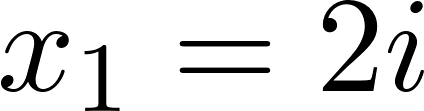
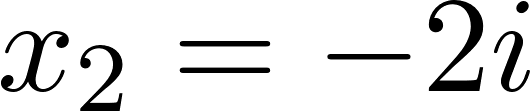
Проведем проверку:
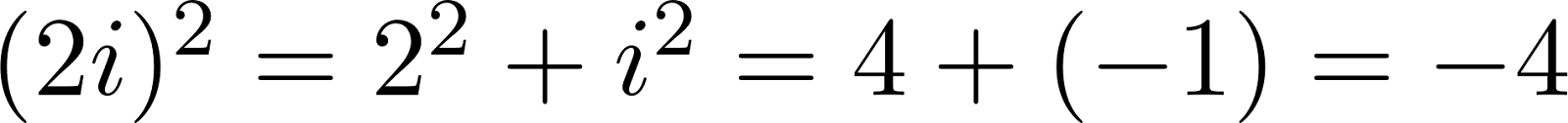

Это был простой пример, а теперь давайте рассмотрим пример посложнее:

Сначала может показаться, что ответ достаточно просто найти, ведь  , но что же в таком случае происходит с
, но что же в таком случае происходит с  , ведь
, ведь  ? Что-то тут не сходится.
? Что-то тут не сходится.
Поскольку для всех значений корня величина модуля одинакова, а меняется лишь его аргумент, все n значений корня располагаются на комплексной плоскости на окружности радиуса  c центром в начале координат. Корни делят эту окружность на n равных частей.
c центром в начале координат. Корни делят эту окружность на n равных частей.
Таким образом  будет иметь модуль 2, а все его корни будут располагаться на окружности в комплексной плоскости с одинаковым равноудаленным интервалом. Стоит отметить тот факт, что длина всех отрезков на окружности - это все еще длина радиуса и она также имеет размер 2, разница лишь в том, где в комплексной плоскости расположено число. На комплексной плоскости это будет выглядеть так:
будет иметь модуль 2, а все его корни будут располагаться на окружности в комплексной плоскости с одинаковым равноудаленным интервалом. Стоит отметить тот факт, что длина всех отрезков на окружности - это все еще длина радиуса и она также имеет размер 2, разница лишь в том, где в комплексной плоскости расположено число. На комплексной плоскости это будет выглядеть так:

Для того, чтобы аналитически рассчитать значение корня необходимо воспользоваться формулой Муавра:
Формула Муавра для комплексных чисел:
Для 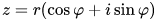
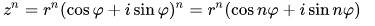 ∀
∀  .
.
Таким образом, для  корни будут находится на
корни будут находится на  , что мы и видели уже на графике.
, что мы и видели уже на графике.
Положительные числа
А что же будет с положительными числами корня n-ной степени? Их тоже будет n штук! В общем-то принцип тут не меняется, их также можно найти по формуле Муавра, давайте сразу приведем ответ для уравнения 

Т.е. решением уравнения х =  будут корни:
будут корни: 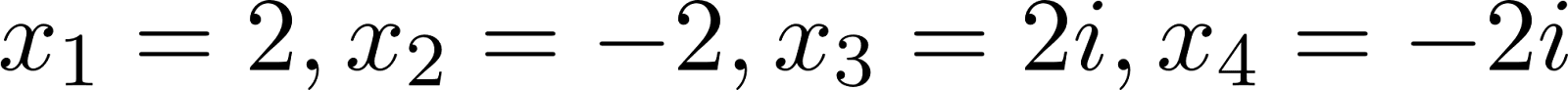
Давайте это проверим:


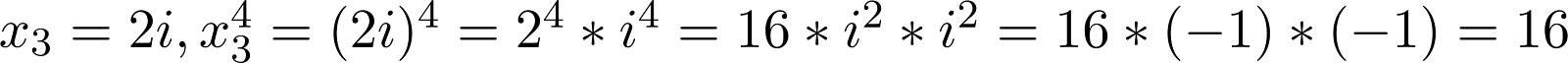

Работает!
Бонусная картинка для тех, кто дочитал до конца:


